Rundungsverfahren - Rundungsdifferenzen?

Die Kurzfassung:

1. Es gibt verschiedene Gründe für Rundungsdifferenzen.
2. Rundungsdifferenzen lassen sich nicht immer vermeiden.

Rundungsdifferenzen beim Datenaustausch

Rundungsdifferenzen sehen Sie in seltenen Fällen, wenn Sie Werte aus ORCA AVA mit von Hand ermittelten Werten oder mit Werten aus Fremdprogrammen vergleichen.

Das liegt meist daran, dass verschiedene Programme verschiedene Datentypen verwenden und eigene Algorithmen zur Berechnung von Werten nutzen. Software-Programmierung ist keine exakte Wissenschaft: es gibt nicht 'den' richtigen Weg, um einen Wert zu ermitteln oder nur einen möglichen Datentyp, der dabei verwendet werden kann.

Zudem sind auch die Beschreibungen von 'neutralen' Datenschnittstellen oft nicht absolut vollständig und eindeutig. Es bleibt ein gewisser Ermessens- oder Interpretations-Spielraum bei der entwicklungstechnischen Umsetzung.

Technische Gründe für Rundungsdifferenzen

Computer können keine unendlich langen Zahlen speichern - auch wenn es manchmal so scheint! Deshalb existieren verschiedene Datentypen mit unterschiedlich vielen Nachkommastellen, um Berechnungen möglichst genau durchführen zu können.

Aus einer Abwägung von Genauigkeit und 'Performance' (Rechengeschwindigkeit) folgt die Auswahl eines bestimmten Datentyps zum Speichern bestimmter Werte.

Wann treten Rundungsdifferenzen auf?

Die technischen Randbedingungen für Rundungsdifferenzen in ORCA AVA lassen sich klar benennen:

1. Es handelt sich um die Ergebnisse von Berechnungen.
2. Bei exakter Berechnung - ohne Begrenzung der Nachkommastellen! - entstehen mindestens 5 Nachkommastellen.
3. Diese 5 Nachkommastellen weisen in der 3. bis 5. Stelle eine ganz bestimmte Zahlenkonstellation auf:
   • die 3. Nachkommastelle ist eine 4 und
   • die 4. Nachkommastelle ist eine 9 und
   • die 5. Nachkommastelle ist eine Zahl größer-gleich 5.
4. Das Ergebnis der Berechnung ist nur mit 2 Nachkommastellen anzugeben.

Beispiel:
Ermittlung von Positionsgesamtpreisen, auf Papier berechnet und auf 2 Nachkommastellen gerundet.

Menge (m)	x EP in EUR	GP in EUR (gerundet)	ORCA AVA
5,982	x 21,39 =	127,95498 (127,95)	127,96
11,464	x 56,39 =	646,45496 (646,45)	646,46

Dieser scheinbare 'Fehler' in ORCA AVA resultiert daraus, dass Rechner keine unendlich langen Zahlen oder Rechenergebnisse speichern können. Es muss immer ein reservierter Speicherplatz (Datentyp) für die Aufnahme einer Zahl oder eines (Zwischen-)Ergebnisses vorhanden sein.

ORCA AVA verwendet den Datentyp 'Currency'. Dieser Datentyp unterstützt 15 Vorkomma- und 4 Nachkommastellen und wird als schneller Datentyp von hoher Genauigkeit für Berechnungen mit Geldbeträgen beschrieben.

Bei den oben genannten Beispielen wird bereits auf Ebene des Datentyps (in den Tiefen des Rechners selbst, ohne dass ORCA AVA das überhaupt mitbekommt!) auf die 4. Nachkommastelle gerundet - einfach weil die Zahl nur mit 4 Nachkommastellen gespeichert werden kann. Dabei wird kaufmännisch (richtig) gerundet:

127,95498 wird zu 127,9550
646,45496 wird zu 646,4550

Da aber dann für den Positionsgesamtpreis EURO mit 2 Nachkommastellen angegeben werden sollen, wird auf die 2. Nachkommastelle (wiederum richtig) kaufmännisch gerundet:

127,9550 wird zu 127,96 EUR
646,4550 wird zu 646,46 EUR

Einheitspreise können Sie in ORCA AVA mit 3 Nachkommastellen angeben. Dies wird auch im Format GAEB XML unterstützt.

Sind technische Rundungsdifferenzen zu vermeiden?

Hier gibt es nur ein klares NEIN! ... man könnte zwar vielleicht spezielle Rundungsdifferenzen vermeiden (durch die Verwendung eines anderen Datentypen), aber man würde dafür andere Rundungsdifferenzen erzeugen (durch die Verwendung dieses anderen Datentypen).

In ORCA AVA werden in rund 400.000 Codezeilen ca. 2.000 Multiplikationen und Divisionen ausgeführt. Eine Umstellung des Datentyps kann zu einer unkalkulierbaren Zahl abweichender Ergebnisse führen, die dann aus Besonderheiten dieses anderen Datentypen resultieren. Beispiel: (1.500.000 / 100) * 81,7 liefert als Gleitkommazahl (single) berechnet den Wert 1.225.499,95422363 gerundet also 1.225.499,95 - exakt berechnet sind es aber 1.225.500,00.

Es würde nicht besser, nur anders. Daher ist eine Umstellung des Datentyps nicht vorgesehen.

Rundungsdifferenzen durch Auf-/Abschläge

Auf-/Abschläge können ebenfalls zu Rundungsdifferenzen führen, besonders, wenn es sich um pauschale Abschläge handelt.

In der gewerkeorientierten Struktur eines Auftrags wird ein pauschaler Abschlag einfach abgezogen. Wenn aber wieder in der Auswertung nach Kostengruppen ein 'bereinigter' Wert ermittelt werden soll, bleibt nur die Möglichkeit, den Aufschlag prozentual auf beteiligte Positionen/Teilmengen umzulegen. Die Rundungsdifferenz im Vergleich von Projekttabelle und zugehöriger KG-Auswertung ist damit so gut wie sicher.

Rundungsdifferenzen bei Auswertungen nach Kostengliederungen

Bei der Auswertung nach Kostengliederungen wird eigentlich nur eine 'Umsortierung' von bestehenden Daten durchgeführt: Aus der gewerkeorientierten Sortierung, z.B. in einem Leistungsverzeichnis, wird anhand der eingetragenen Kostengruppen (bei Positionen oder Teilmengen von Positionen) in die Ordnung der jeweiligen Kostengliederung umsortiert.

Es können Abweichungen zwischen den Summen der Kostengruppen und der Projektsumme auftreten: In der Projektsumme (z.B. AMP) wird für jede Position die Gesamt-Menge mit dem EP multipliziert - in der Auswertung nach Kostengliederungen werden Mengenanteile einer Position mit dem EP multipliziert, gerundet und dann zur KG-Summe addiert.

Beispiel: Kostengruppen-Zuordnungen in Teilmengen

Position Stahlrohre DN 50, Gesamtmenge 20m, je 17,55 EUR = 351,00 EUR ... im Mengensplitting/Kostensplitting aufgeteilt in 2 Kostengruppen:

12,5m in KG 412 Abwasseranlagen:
12,5 x 17,55 = 219,375 - gerundet: 219,38 EUR

7,5m in KG 421 Wärmeerzeugungsanlagen:
7,5 x 17,55 = 131,625 - gerundet: 131,63 EUR

KG-Summe: 351,01 EUR => 0,01 EUR Rundungsdifferenz in der KG-Auswertung.

In der AMP prüfen Sie, was der Auftragnehmer für diese Leistung zu erhalten hat - darum ist der Positionswert der entscheidende. Die Kostengruppenauswertungen sind dagegen 'akademische' Betrachtungen...

Spalten oder Zeilen?

Eine weitere Quelle für Rundungsdifferenzen (oder gefühlt-falschen Werten) resultiert aus der Abwägung, ob die Ergebnisse von Spaltenberechnungen einen höheren Stellenwert als die Ergebnisse von Zeilenberechnungen haben, bzw. ob Teilmengen höher zu bewerten sind als Gesamtmengen.

Beispiel

Für eine Position erfassen Sie in der Aufmaßprüfung (AMP) mehrere Teilmengen. Der EP ist 21,39 EUR.
Die Teilmengen werden den Kostengruppen 1, 2 und 3 wie folgt zugeordnet:

Teilmenge AMP	x EP	GP in ...	KG
1,697	x 21,39 =	36,30	1	* Die Summe für diese Position in der KG 2: 29,95 + 29,95 = 59,90 ... richtig. Wirklich?
1,400	x 21,39 =	29,95*	2
1,400	x 21,39 =	29,95*	2
8,95	x 21,39 =	191,44	3
S 13,447		S 287,64

Diese Werte sehen Sie, wenn Sie eine KG-Auswertung mit Teilmengen ausgeben.

In der AMP selbst wird aus den Teilmengen immer nur eine Gesamt-Positionsmenge errechnet (13,477) und mit dem EP (21,39) multipliziert.
Ergebnis: 287,631333 ... gerundet: 287,63 EUR - gegenüber 287,64 EUR in der KG-Auswertung. Diesen einen Cent Rundungsdifferenz zwischen AMP-Wert und KG-Wert kennen wir ja schon.

Es geht aber noch weiter:

In der Kostengruppen-Auswertung möchten wir nun nicht die Teilmengen, sondern die Gesamtmengen für die Positionen ausgeben.
Was steht dann in der KG 2 für diese Position in der Zeile:

2,800 x 21,39 = 59,90 ??
...das wäre die GP-Addition der Teilmengenkosten oder:
2,800 x 21,39 = 59,89 ??
... das wäre die Multiplikation der (Gesamt-)Teilmenge mit dem EP.

Sie erkennen das Dilemma?

Teilrechnungen mit kumulativer Rechnungsfreigabe

Eine weitere Feinheit beim Anlegen von Teilrechnungen: Nettobetrag Gesamt bezogen auf das Aufmaß Gesamt (= kumulative Rechnungsfreigabe)

Bei einer schrittweisen Aufmaßprüfung werden hierbei bei jeder neuen Teilrechnung die aktuell erreichten Gesamtwerte sowohl für die Mengen, als auch für die Nettobeträge Gesamt errechnet! Bereits erfolgte Zahlungen werden vom Nettobetrag Gesamt der aktuellen Rechnung abgezogen. D.h. sobald aus Vorgänger-Teilrechnungen schon Werte vorhanden sind (die auch nicht ganzzahlig waren!), können Rundungsdifferenzen entstehen.

Beispiel:

Zwei Teilrechnungen (TR), die Position hat einen EP von 46,22 EUR.

	Zuwachsmenge	x EP	exakt (gerundet)	ORCA AVA Gesamt
1. TR	5,200	x 46,22 =	240,344 (...,34)	240,34
2. TR	278,600	x 46,22 =	12.876,892 (...,89)	12.876,90

... rechnet ORCA AVA falsch? Nein! ORCA AVA berechnet auch den Zahlungsbetrag für die 2.TR über die erreichte Gesamtmenge und nicht über die Zuwachsmenge:

5,2 + 278,6 = 283,8 (= Aufmaß) multipliziert mit dem EP 46,22 ergibt: 13.117,236
... gerundet: 13.117,24 EUR

Der Wert, der als Nettobetrag gesamt für die Zuwachsmenge in der zweiten TR angezeigt wird, ist nicht aus der Multiplikation 'Zuwachsmenge 2. TR x EP' gebildet, sondern aus der Differenz:

Nettobetrag Gesamt für Aufmaß abzüglich Nettobetrag Gesamt bisheriger Aufmaßstand = Nettobetrag Gesamt (= Kostenzuwachs) dieser Teilrechnung

... d.h. im Beispiel: 13.117,24 abzüglich 240,34 = 12.876,90 EUR 

Bei umgekehrter Reihenfolge der TRs würde sich folgerichtig ergeben:

	Zuwachsmenge	x EP	exakt (gerundet)	ORCA AVA
1. TR	278,600	x 46,22 =	12.876,892 (..., 89)	12.876,89
2. TR	5,200	x 46,22 =	240,344 (...,34)	240,35

... hier: 13.117,24 abzüglich 12.876,89 = 240,35 EUR!

Das ist aber nicht tragisch: Solche Rundungsdifferenzen bei Teilrechnungen in Rechnungs-Sequenzen werden beim Anlegen der Schlussrechnung ausgeglichen, da sich hier der Nettobetrag Gesamt immer auf das Gesamt Aufmaß bezieht!

Formales (Bau-)Hintergrundwissen

Im Bereich der Aufmaßprüfung / Mengenermittlung gibt es einige Regelwerke, die (historisch teilweise widersprüchliche) Forderungen in Bezug auf die anzugebenden Nachkommastellen und das anzuwendende Rundungsverfahren enthalten.

1. In der aktuellen VHB 2017 (Stand Juli 2019) finden sich keine Angaben zu Nachkommastellen bei Mengen.
   Eine Angabe zu Nachkommastellen findet sich nur noch auf Preise bezogen: max. 3 Nachkommastellen sind möglich.

   In den Vorgängerversionen des Vergabehandbuch fand sich (z.B. 2008 (Bund) - VHB) unter
   "Zusätzliche Vertragsbedingungen für die Ausführung von Bauleistungen Einheitliche Fassung" in Ziffer 10.4 noch die Angabe:
   " Bei Abrechnungen sind Längen und Flächen mit zwei Stellen nach dem Komma, Rauminhalte und Massen mit drei Stellen nach dem Komma anzugeben."

2. Die REB 23.003 regelt 'Mengenberechnungen' und den Datenaustausch - Hier ist in Ziffer 2.4 'Rundung' gefordert, Mengen mit 3 Nachkommastellen anzugeben (und zwar generell - was bis zur Herausgabe des VHB 2017 nicht gewünscht war).
3. In der oft für Rundungsregeln zitierten Norm DIN 1333 'Zahlenangaben' wird als "Anwendungsbereich und Zweck" (Seite 1) definiert, dass die Norm "...festlegt, wie Zahlen im täglichen Leben in Wirtschaft, Technik und Wissenschaft geschrieben werden sollen" - der letzte Satz dieses Abschnitts besagt:
   "Diese Norm gilt nicht für die interne Zahlendarstellung von Computern."
   Die DIN 1333 gesteht auch in Ziff. 4.2 'Festlegen der Rundestelle' zu:
   "Die Rundestelle kann … sich aus technischen Gründen ergeben (letzte Stelle der Ergebnisablage im Speicher einer Datenverarbeitungsanlage)."

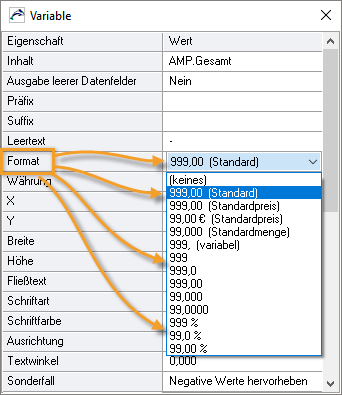
Für die Ausgaben gibt es bei jeder Variablen (Datenfeld) die Eigenschaft Format, die eine Vielzahl an möglichen Anzeigeformaten bietet. Bedenken Sie aber, dass ein 'unpassendes' Anzeigeformat auch den Anschein eines vermeintlichen Fehlers erwecken kann.

Diese Formate werden nur für die Anzeige in der Ausgabe benutzt! Intern und im Datenaustausch werden immer die vorhandenen, bzw. geforderten Nachkommastellen benutzt und übergeben!

Fehlerbetrachtung bei Rundungsdifferenzen

Wir sprechen hier oft nur von einem Cent Differenz - der aber zu Diskussionen führt. Nicht zuletzt, weil von Computern eine absolute Richtigkeit erwartet wird. Oft geht es aber nur darum, sich im realen Leben auf akzeptable Näherungen zu einigen.

Beispiel Mathematik: Umrechnen von Brüchen zu Dezimalzahlen

10 geteilt durch 3 ist 3 1/3 oder 3,3333 Periode - das kann theoretisch exakt angegeben werden.
Will man aber 10 Euro auf drei Personen verteilen, so rundet man auf 2 Stellen: 3,33 EUR.
Aber: 3 x 3,33 zurückgerechnet, ergibt 9,99 EUR.
Es bleibt also praktisch ein Cent übrig - falls man gerecht verteilen will. Wer bekommt den Cent?

Beispiel Aufmaßprüfung: Toleranzen

Sehen wir uns das Rechenbeispiel aus den 'Technischen Gründen' noch mal an:

11,464 m	x 56,39 EUR =	646,46	ORCA AVA
11,464 m	x 56,39 EUR =	646,45	(Papier)

Wir haben in ORCA AVA einen Cent Differenz gegenüber dem 'Papier'-Wert.

1. Überlegung: Wie würde sich ein 'Fehler' durch eine Maßtoleranz auswirken?
   Maßtoleranzen sind z.B. nach DIN 18202 'Toleranzen im Hochbau' geregelt:
   Bei Nennmaßen von über 6 m bis 15 m ist eine Maßtoleranz von +/- 20 mm erlaubt.
   Wir rechnen mit einer Abweichung von nur 1 mm:

   11,465 m x 56,39 EUR = 646,51 EUR
   ... 6 Cent Differenz gegenüber dem 'Papier'-Wert (ist natürlich abhängig vom EP).

2. Überlegung: Wie würde sich eine Abrechnung gemäß VHB mit 2 Nachkommastellen statt nach REB mit 3 Nachkommastellen auswirken?
   Also: 11,464 abrunden, dann erhalten wir...

   11,460 m x 56,39 EUR = 646,23 EUR
   ... 23 Cent Differenz gegenüber dem 'Papier'-Wert (auch abhängig vom EP).

Damit sind wir bei der Realität am Bau angelangt...!

Wie vermeiden Sie Diskussionen über Cent-Differenzen und Rundungsfehler?

Vereinbaren Sie mit Ihren Bauherren und Auftragnehmern sinnvolle, geforderte bzw. zulässige Genauigkeiten im Aufmaß und bei der Rundung!

Denken Sie dabei auch nicht nur an einzelne Werte, sondern an die Projektsummen: Erfahrungsgemäß heben sich Rundungsdifferenzen auch gerne gegenseitig auf, so dass in der Gesamtsumme nur eine kleine Differenz bleibt.